Bellman k-segmentation algorithm

Written 2014 Oct 19 — Tags: Algorithms, Dynamic Programming
Using Julia circa v0.3

The Bellman $k$-segmentation algorithm generates a segmented constant-line fit to a data series, but in trying to learn and implement this algorithm, I found it difficult to find the segmentation algorithm rather than the [apparently more common] $k$-means algorithm, so in this article I describe and provide code for the $k$-segmentation algorithm.

Introduction

Richard Bellman is probably best known for his work on the Bellman–Ford algorithm (which generates the single-source shortest path on a weighted graph), but his biggest contribution to algorithms was the development of dynamic programming. In short, dynamic programming is applied to algorithms which need to solve a problem by considering smaller sub-problems, but these sub-problems are often repeated across many different cases. By using some extra memory to remember the answers to already-seen answers, the run-time can be vastly decreased.

The $k$-segmentation algorithm we want to describe is exactly one such example of a dynamic programming problem. Before we can understand that this is true, though, we need to define exactly what we want to achieve with this algorithm. Consider a series of $N$ data points, such as in Fig. 1.1. The data would not be represented well by a single line, so the common least-squares regression is insufficient. Instead, we might choose to model the data using several constant line segments. For example, visually it is easy to see that the data between about 6 and 10 could be approximated well by a line segment passing through them along the x-axis.

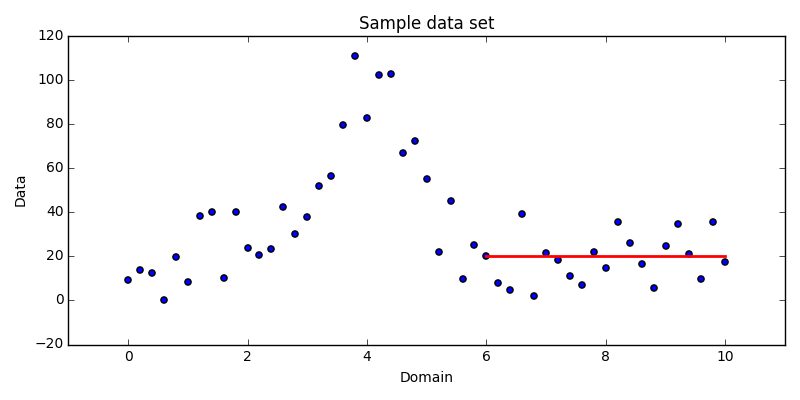
A sample data set which is not characterized well by a single linear fit. Visually, some line line segments (such as shown in red) are easy to guess, but we want to quantify and create an algorithm which can create a “good” fit over the entire domain.

In general, though, we can’t do this by hand for all data. Instead, we want a way to quantify how well a fit models the given data and from that, determine what the best set of line segments are to use. In more specific terms, we want to determine a $k$ segments piece-wise constant regression (where $1\le k \le N$) of the $N$ data points. (In general, $k=1$ with a single degree of freedom is a poor choice since it’s actually worse than the 2 degrees of freedom least squares fit we already rejected, and $k=N$ doesn’t model the data at all since a single line segment can be used for each data point.)

Formally, we’ll define the problem as:

Given $N$ data points $\{x_1, x_2, \ldots, x_N\}$, the $k$-segmentation algorithm generates a piece-wise constant sequence of line segments $s_j$ where $j = 1,\ldots,k$ with $s_j = (b_j, l_j, \bar s_j)$. Each line segment $s_j$ covers the span beginning with $x_{b_j}$ and ending at $x_{l_j}$ (naturally with $b_j \le l_j$, $b_1 = 1$, and $l_k = N$) and represents those data points by the mean of the span $\bar s_j = \operatorname{mean}(\{ x_{b_j}, \ldots, x_{l_j} \})$. The quality of the fit is evaluated by minimizing the total fit error, \begin{align} E_S = \sum_{i=1}^N w_i (x_i - \bar x_i)^2 \end{align} where $\bar x_i = \bar s_j$ for $b_j \le i \le l_j$ and $w_i$ is a weighting factor for each data point.

This particular form of the error function is chosen for its applicability to dynamic programming solutions; you can see a much longer discussion showing this fact in my article on choosing a computationally efficient distance function.

Dynamic programming approach

Building from the ground up, there are two conditions we need to demonstrate the $k$-segmentation problem meets before we can apply dynamic programming techniques to the implementation:

  1. Optimal substructure: The solution must rely on a subproblem being an optimal solution for the total solution to also be optimal.

  2. Overlapping subproblems: The solutions method must share a small subset of common subproblems which are needed many times. In contrast, non-overlapping subproblems leads to the simpler divide-and-conquer paradigm.

Optimal substructure

For this problem, the most obvious way to demonstrate the optimal substructure property is to consider successive values of $1 \le k' \le k$ through induction to find an appropriate recursion relation.

Let the notation $E_S[i,k']$ represent the segmentation error over the data points $\{x_1,\ldots,x_i\}$ using $k'$ segments, and let $E[i,j]$ be the error in representing the points $\{x_i,\ldots,x_j\}$ using just the mean of the data.

For the trivial case of $k' = 1$, we simply fit a single line segment as the mean over all data points, with an associated error $E_S[N,1] = E[1,N]$. Next, allow a second line segment to be used. The question becomes at which point $i$ do we add the line segment so that there are two line segments from $1...i$ and $(i+1)...N$. The error in this case is then

\begin{align*} E_S[N,2] = \min_{1\le i\le N} ( E[1,i] + E[i+1,N] ) \end{align*}

Moving up to $k' = 3$ is more complicated yet. Now when we append a line segment to the end, we have two boundaries we need to determine. Instead of thinking of the problem as finding two boundaries, though, we can take the viewpoint that we’re still adding a segment to the end, but simply over a longer sequence. (I presciently defined $E_S$ with this in mind since we can specify where the end of the data sequence is.) In this light, let’s recast the previous two cases in terms of “growing” sequences:

\begin{align*} E_S[i,1] &= E[1,i] \\ E_S[i,2] &= \min_{1\le j \le i} ( E_S[j-1,1] + E[j,i] ) \\ \end{align*}

The extension to the case $k' = 3$ should now be obvious, so through induction, let us skip straight to the generic recursion relation.

\begin{align} E_S[i,k'] &= \min_{1\le j \le i} ( E_S[j-1,k'-1] + E[j,i] ) \label{eqn:recurse} \end{align}

The optimal substructure in the problem is hopefully obvious in this form: in order to know the optimal $k'$-segmentation solution, we need to know what the optimal $(k'-1)$-segmentation solutions are. Because these are recursion relations, storing the answer very rapidly saves computational time over descending the recursion tree every time a particular answer is needed.

Overlapping subproblems

We can also very quickly demonstrate how the algorithm satisfies the overlapping subsproblems property by inspecting Eq. $\ref{eqn:recurse}$. The $E[j,i]$ term can be required many, many times for a particular choice of $(j,i)$, and this by definition is an overlapping subproblem. Maybe less obviously, the $E_S[j-1,k'-1]$ term also demonstrates the overlapping subproblem property. If you remember to consider it in terms of a recursion tree, the child subproblems (at the $k'-1$ level) will depend on overlapping solutions at the grandchild ($k'-2$) level.

Algorithm design

Before continuing, you can download the IJulia notebook used to generate the sample data, analyze the data, and plot the figures. If you want to play around with the algorithms more, this notebook already contains a copy of the code we will be developing.

The rest of this article will deal with the details of the algorithm design to solve this problem. There are three major parts: pre-computing the error for subsequences with respect to their mean, calculating the segmentation errors, and reconstructing the solution. We’ll take each part in turn.

Subsequence errors

As required in the recursion relation we described in Eq. $\ref{eqn:recurse}$, we need to know the error of representing any arbitrary subsequence by its mean. For this purpose, we use distance function described in another article I’ve written (which is very similar to the mean-squared error, differing in the overall normalization and inclusion of a weighting term). For a detailed description, see that article, but here we’re just concerned with the results:

\begin{align} W[i,j] &\equiv \sum_{k=i}^j w_k \\ S[i,j] &\equiv \sum_{k=i}^j w_k x_k \\ Q[i,j] &\equiv \sum_{k=i}^j w_k {x_k}^2 \end{align}
\begin{align} E[i,j] &= Q[i,j] - \frac{S[i,j]^2}{W[i,j]} \end{align}

The important part to note here is that the error is defined in terms of three partial sums $W[i,j]$, $S[i,j]$, and $Q[i,j]$. These are useful because as simple sums, any two arbitrary (disjoint) subsequences can be combined with a three quick additions of the partial sums and then a recalculation of the error term. In the other article, I show that a convenient choice of growing longer subsequences is to just append each subsequence with the next element, as graphically shown in Fig. 3.1. The red arrows point from the two terms combined in each partial sum to generate the new longer subsequence partial sums.

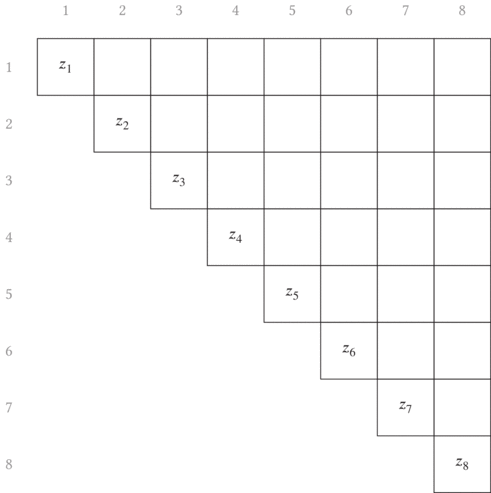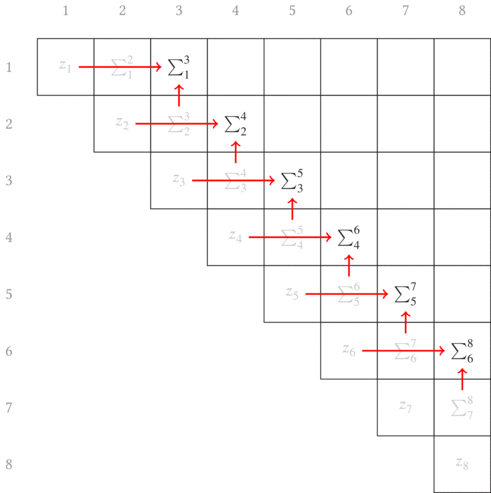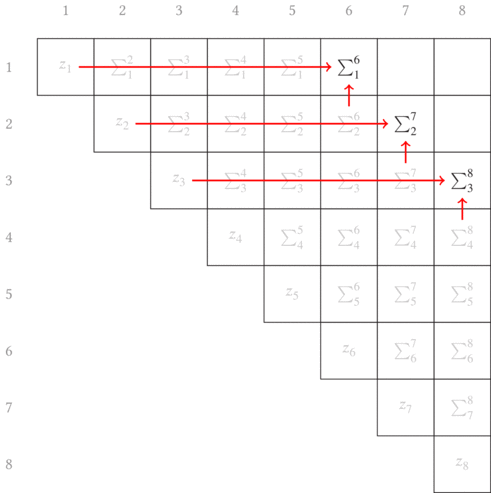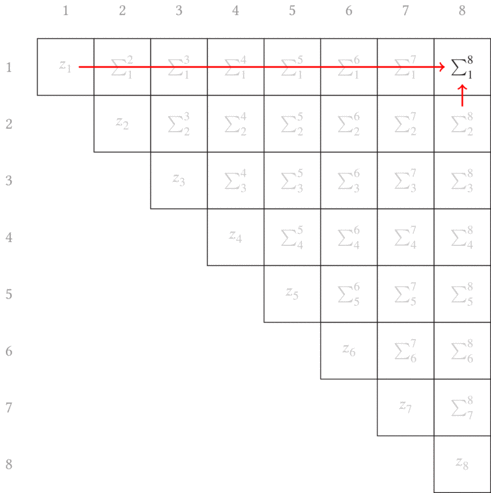
Animation which demonstrates the characteristic up-sweep of the chosen growth scheme. The arrows show which two elements were summed to produce each new answer. A different choice of how to split the work would result in a different pattern of arrows or even a different sweep direction along the matrix.

Another thing to note is that this is shown as a matrix. With our errors being defined in terms of indices of the beginning and ending of a subsequence, it is convenient (both visually and progmatically) to consider the indices as the row and column into a matrix. (In a similar manner, we’ll later build a non-square matrix for the total segmentation error.)

Now to dig into the code. Since we need the error over all subsequences for every iteration of the recursion relation, it makes sence to precompute this matrix, so we define a function prepare_ksegments which will produce the errors. The only two inputs we need are the data series and a matching list of weights:

function prepare_ksegments(series::Array{Float64,1}, weights::Array{Float64,1})
    N = length(series);

Next we initialize the partial sums and error matrices, but we do so by filling the diagonal immediately since it’s comprised of single element only data products. The error matrix is just generated as an empty matrix.

    wgts = diagm(weights);
    wsum = diagm(weights .* series);
    sqrs = diagm(weights .* series .* series);

    dists = zeros(Float64, N,N);

Hopefully the animated sequence in Figure 3.1 makes the form of the loops clear: we are going to proceed right-ward from the diagonal and as you go, there are less rows to move through on each iteration. The contents of the loop should be self-explanatory and just encapsulate the contents of the sums shown above.

    for δ=1:N
        for l=1:(N-δ)
            r = l + δ;

            wgts[l,r] = wgts[l,r-1] + wgts[r,r];
            wsum[l,r] = wsum[l,r-1] + wsum[r,r];
            sqrs[l,r] = sqrs[l,r-1] + sqrs[r,r];

            dists[l,r] = sqrs[l,r] - wsum[l,r]*wsum[l,r]/wgts[l,r];
        end
    end

Finally, we can note that everything we need to calculate the means of each subsequence is already being stored in the temporary partial sum matrices, and since we’ll need the mean values of particular subsequences later, we can precompute those as well. Inserting the appropriate matrix initialization and calculations for the means, the final function in total takes the form:

function prepare_ksegments(series::Array{Float64,1}, weights::Array{Float64,1})
    N = length(series);

    # Pre-allocate matrices
    wgts = diagm(weights);
    wsum = diagm(weights .* series);
    sqrs = diagm(weights .* series .* series);

    # Also initialize the outputs with sane defaults
    dists = zeros(Float64, N,N);
    means = diagm(series);

    # Fill the upper triangle of dists and means by performing up-right
    # diagonal sweeps through the matrices
    for δ=1:N
        for l=1:(N-δ)
            # l = left boundary, r = right boundary
            r = l + δ;

            # Incrementally update every partial sum
            wgts[l,r] = wgts[l,r-1] + wgts[r,r];
            wsum[l,r] = wsum[l,r-1] + wsum[r,r];
            sqrs[l,r] = sqrs[l,r-1] + sqrs[r,r];

            # Calculate the mean over the range
            means[l,r] = wsum[l,r] / wgts[l,r];
            # Then update the distance calculation. Normally this would have a term
            # of the form
            #   - wsum[l,r].^2 / wgts[l,r]
            # but one of the factors has already been calculated in the mean, so
            # just reuse that.
            dists[l,r] = sqrs[l,r] - means[l,r]*wsum[l,r];
        end
    end

    return (dists,means)
end

Segmentation errors

With the subsequence errors done, we can now work on calculating the segmentation errors. As an implementation choice, I’ve done all of this work directly in the regression interface regress_ksegments. The regression interface again needs the data and weights, and it also to know how many segments to fit to the data. We then immediately calculate and store the subsequence errors.

function regress_ksegments(series::Array{Float64,1}, weights::Array{Float64,1}, k::Int)
    N = length(series);

    (one_seg_dist,one_seg_mean) = prepare_ksegments(series, weights);

Instead of a square look-up matrix for the subsequence error $E[i,j]$ as we used in the previous section, the total segmentation error $E[i,k']$ is stored in a non-square matrix. There are as many rows as possible values of $k'$, but you’ll notice that instead of a width of $N$ for the number of data points, I’ve added an extra column. This extra “ghost” column is logically placed on the left to allow the algorithm to explore the possibility that the best possible fit includes no previous segments and instead is best fit by a single average over all elements.

At this point, the ghost column is already initialized (to zero) since we want there to be no consequence for choosing to not use previous segments—in most conceivable situations, the high cost of using a single subsequence average will be disfavored due to the high cost. The other initialization we need is for the case where $k'=1$. As we already showed, this is just the single subsequence error, so we can copy that from $E[1,i]$.

    k_seg_dist = zeros(Float64, k, N+1);
    k_seg_path = zeros(Int, k, N);
    k_seg_dist[1,2:end] = one_seg_dist[1,:];

The k_seg_path variable we initialized is used at the end for reconstructing the optimal solution. A common characteristic of dynamic programming problems is that they also require some tracking information to solve the full problem. Without this matrix, we could report the error of the optimal $k$-segmentation regression, but we wouldn’t actually be able to show what that regression is. The index into the matrix is the right (inclusive) boundary of a segment, and the value it contains is the left (exclusive) boundary. This means that the correct initialization for all $k'=1$ regressions stretch to the beginning of the list. Likewise, if we use $N = k’$, then the left boundary points to the previous elements. (The complicated syntax in the second line below just indexes this “diagonal” in a single line of code.)

    k_seg_path[1,:] = 0;
    k_seg_path[sub2ind(size(k_seg_path),1:k,1:k)] = (1:k) - 1;

We make use of the fact that the recursion relation in Eq. $\ref{eqn:recurse}$ can be transformed into a loop (also known as tail recursion) and just start at $k'=2$ (remember, we initialized the first case) and work our way up to $k'=k$. The inner loop runs over all possible choices of the final subsequence length, and inside that, we just sum the segmentation and single-subsequence errors. We then find the minimum total error and record the location into the path reconstruction matrix and error value into the total error matrix.

    for p=2:k
        for n=p:N
            choices = k_seg_dist[p-1, 1:n] + one_seg_dist[1:n, n]';

            (bestval,bestidx) = findmin(choices);
            k_seg_path[p,n] = bestidx - 1;
            k_seg_dist[p,n+1] = bestval;
        end
    end

At this point, we know the cost of the optimal solution (which is stored in $E_S[N,k]$) but what we really want to know is what the optimal regression is. The final bit of code does this by constructing a return array of length $N$ with every data point set to its appropriate mean.

We start with the right-hand side pointing to the $N$-th element for the solution with $k$ segments. The path matrix tells us where the left-hand side of the optimal segment is to be located, so we fill in the regression values over that segment with the appropriate mean. We then repeat for the $k-1$ remaining segments by moving up a row in the matrix and start with the right-hand side to the immediate left of the just-generated segment.

    reg = zeros(Float64, size(series));

    rhs = length(reg);
    for p=k:-1:1
        lhs = k_seg_path[p,rhs];
        reg[lhs+1:rhs] = one_seg_mean[lhs+1,rhs];
        rhs = lhs;
    end

Putting all of these pieces together, along with some error checking and some convenience interfaces that let us forgo explicitly stating the weighting if we want uniform weighting, we have:

function regress_ksegments{T<:Number}(series::AbstractArray{T,1}, k::Int)
    # Fill in weights with default value if not given.
    weights = ones(Float64, size(series)) / length(series);

    return regress_ksegments(float(series),weights,k)
end

function regress_ksegments{T1<:Number,T2<:Number}(series::AbstractArray{T1,1}, weights::AbstractArray{T2,1}, k::Int)
    return regress_ksegments(float(series),float(weights),k)
end

function regress_ksegments(series::Array{Float64,1}, weights::Array{Float64,1}, k::Int)

    # Make sure we have a row vector to work with
    if (length(series) == 1)
        # Only a scalar value
        error("series must have length > 1")
    end

    # Ensure series and weights have the same size
    if (size(series) != size(weights))
        error("series and weights must have the same shape")
    end

    # Make sure the choice of k makes sense
    if (k < 1 || k > length(series))
        error("k must be in the range 1 to length(series)")
    end

    N = length(series);

    # Get pre-computed distances and means for single-segment spans over any
    # arbitrary subsequence series(i:j). The costs for these subsequences will
    # be used *many* times over, so a huge computational factor is saved by
    # just storing these ahead of time.
    (one_seg_dist,one_seg_mean) = prepare_ksegments(series, weights);

    # Keep a matrix of the total segmentation costs for any p-segmentation of
    # a subsequence series[1:n] where 1<=p<=k and 1<=n<=N. The extra column at
    # the beginning is an effective zero-th row which allows us to index to
    # the case that a (k-1)-segmentation is actually disfavored to the
    # whole-segment average.
    k_seg_dist = zeros(Float64, k, N+1);
    # Also store a pointer structure which will allow reconstruction of the
    # regression which matches. (Without this information, we'd only have the
    # cost of the regression.)
    k_seg_path = zeros(Int, k, N);

    # Initialize the case k=1 directly from the pre-computed distances
    k_seg_dist[1,2:end] = one_seg_dist[1,:];

    # Any path with only a single segment has a right (non-inclusive) boundary
    # at the zeroth element.
    k_seg_path[1,:] = 0;
    # Then for p segments through p elements, the right boundary for the (p-1)
    # case must obviously be (p-1).
    k_seg_path[sub2ind(size(k_seg_path),1:k,1:k)] = (1:k) - 1;

    # Now go through all remaining subcases 1 < p <= k
    for p=2:k
        # Update the substructure as successively longer subsequences are
        # considered.
        for n=p:N
            # Enumerate the choices and pick the best one. Encodes the recursion
            # for even the case where j=1 by adding an extra boundary column on the
            # left side of k_seg_dist. The j-1 indexing is then correct without
            # subtracting by one since the real values need a plus one correction.
            choices = k_seg_dist[p-1, 1:n] + one_seg_dist[1:n, n]';

            (bestval,bestidx) = findmin(choices);

            # Store the sub-problem solution. For the path, store where the (p-1)
            # case's right boundary is located.
            k_seg_path[p,n] = bestidx - 1;
            # Then remember to offset the distance information due to the boundary
            # (ghost) cells in the first column.
            k_seg_dist[p,n+1] = bestval;
        end
    end

    # Eventual complete regression
    reg = zeros(Float64, size(series));

    # Now use the solution information to reconstruct the optimal regression.
    # Fill in each segment reg(i:j) in pieces, starting from the end where the
    # solution is known.
    rhs = length(reg);
    for p=k:-1:1
        # Get the corresponding previous boundary
        lhs = k_seg_path[p,rhs];

        # The pair (lhs,rhs] is now a half-open interval, so set it appropriately
        reg[lhs+1:rhs] = one_seg_mean[lhs+1,rhs];

        # Update the right edge pointer
        rhs = lhs;
    end

    return reg
end

Example regressions

Using the same data as shown in the introduction, we can now apply a $k$-segmentation regression on the data. Here I’ve chosen to show how the regression changes under two choices of the weighting. The first case is for uniform weighting, shown in Fig. 4.1.

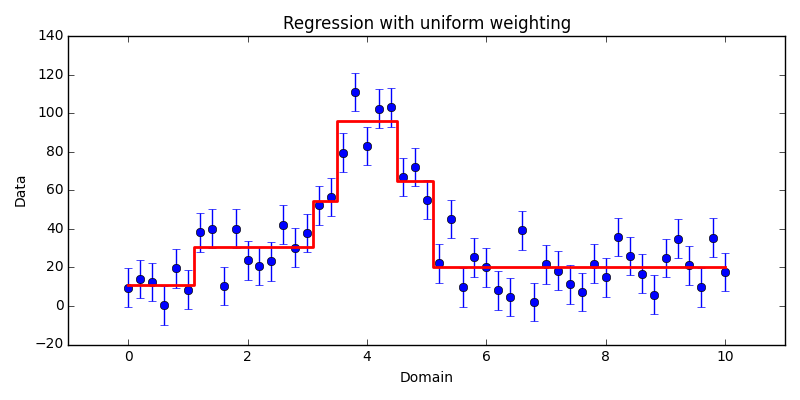
A $k$-segmentation regression applied to our sample data set using uniform weighting. Here, the uniform weight factor was chosen to be 10 simply for visualization purposes; the default weight factor would have instead chosen 0.0196 corresponding to $1 / N$.

The second case shows the affect of weighting the data non-uniformly. The particular weighting choice corresponds to statistical counting error estimate—if the value of a particular bin is $I$, we expect the error on the counts to be $\sqrt{I}$ and correspondingly choose a weight which is the reciprocal square error ($1/I$). In this case we see that the segments are pulled to different locations because the low-error data points incur a larger regression error if they are not fit well than the points with large error.

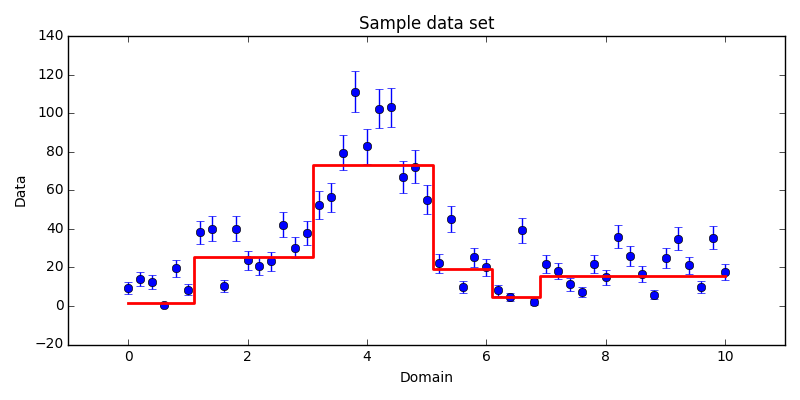
A $k$-segmentation regression applied to our sample data set using counting statistics error and weight estimates on each data point. The regression appropriately changes to minimize the regression error incurred.
  1. Niina Haiminen, Aristides Gionis, & Kari Laasonen. “Algorithms for unimodal segmentation with applications to unimodality detection.” Knowledge and Information Systems, 2008, Vol.14(1), pp.39-57 DOI: 10.1007/s10115-006-0053-3